Signage and Infusion Points
Each sub-slot in both the challenge chain and the reward chain is divided into 64 smaller VDFs. Between each of these smaller VDFs is a point called a signage point. Timelords publish the VDF output and proof when they reach each signage point.
The challenge and reward chains both have signage points. The infused challenge chain, however, does not.
The signage points occur every 9.375 seconds (64 signage points per 600-second sub-slot). The number of iterations between each signage point is sp_interval_iterations, which is equal to sub-slot_iterations / 64.
The challenge at the start of the sub-slot is also a valid signage point. As each of the 64 signage points in the sub-slot is reached, those points are broadcast, starting from the fastest timelord's full node, and propagating to every other full node on the network.
Farmers receive these signage points and compute a hash for each plot, at each signage point. If the hash starts with nine zeros, the plot passes the filter for that signage point, and can proceed. This disqualifies around 511/512 of all plot files in the network, for that signage point. The formula to compute the filter hash is:
plot filter bits = sha256(plot id + sub slot challenge + cc signage point)
The proof of space challenge is computed as the hash of the plot filter bits:
PoSpace challenge = sha256(plot filter bits)
Using this challenge, the farmers fetch quality strings for each plot that made it past the filter. Recall that this process requires around seven random disk seeks, which takes around 70 ms on a slow HDD. The quality string is a hash derived from part of the proof of space (but the whole proof of space has yet to be retrieved).
For both of our previous example, as well as the next example, we'll use the following values:
- sub-slot_iterations = 100,000,000
- sp_interval_iterations =
sub-slot_iterations/ 64 = 1,562,500
The farmer computes the required_iterations for each proof of space. If the requirediterations < sp_interval_iterations, the proof of space is eligible for inclusion into the blockchain. At this point, the farmer fetches the entire proof of space from disk (which requires 64 disk seeks, or 640 ms on a slow HDD), creates an unfinished block, and broadcasts it to the network. If the _required_iterations < sp_interval_iterations, the proof of space is eligible for inclusion into the blockchain. At this point, the farmer fetches the entire proof of space from disk (which requires 64 disk seeks, or 640 ms on a slow HDD), creates an unfinished block, and broadcasts it to the network.
For the vast majority of eligible plots, required_iterations will be far too high, since on average 32 will qualify for the whole network for each 10-minute sub-slot. This is a random process so it's possible (though unlikely) for a large number of proofs to qualify. Any plot that does meet the required_iterations for a signage point will qualify as there is no rivalry between winning plots.
The exact method for required_iterations is the following:
sp_quality_string = sha256(quality_string + cc_signage_point)
required_iterations = (difficulty
* difficulty_constant_factor
* int.from_bytes(sp_quality_string, "big", signed=False)
// pow(2, 256) * expected_plot_size(size))
The difficulty constant factor is based on the initial constants of the blockchain. For Chia, it is 2^67. The difficulty varies per epoch, as explained in Section 3.11 'Section 3.11: Epochs and Difficulty Adjustment'). As you can see, the sp_quality_string is converted into a random number between 0 and 1, by dividing it by 2^256, and then multiplied by the plot size.
For consensus purposes, the expected_plot_size is ((2 * k) + 1) * (2 ** (k - 1))., where k>=32<50. The actual plot size is that value times a constant factor, in bytes. This is because each entry in the plot is around k+0.5 bits, and there are around 2^(k) entries. The actual plot size is that value times a constant factor, in bytes. This is because each entry in the plot is around k+0.5 bits, and there are around 2 ** k entries.
The signage_point_iterations is the number of iterations from the start of the sub-slot to the signage point.
The infusion_iterations is the number of iterations from the start of the sub-slot at which the block with at least the required quality can be included into the blockchain. This is calculated as: This is calculated as:
infusion_iterations = ( signage_point_iterations + 3 * sp_interval_iterations + required_iterations) % sub-slot_iterations
Therefore, infusion_iterations will be between 3 and 4 signage points after the current signage point. Farmers must submit their proofs and blocks before the infusion point is reached. The modulus is there to allow overflows into the next sub-slot, if the signage point is near the end of the sub-slot. This is expanded on in Section 3.9 'Section 3.9: Overflow Blocks and Weight').
More information on infusion points is available in the VDFs page.
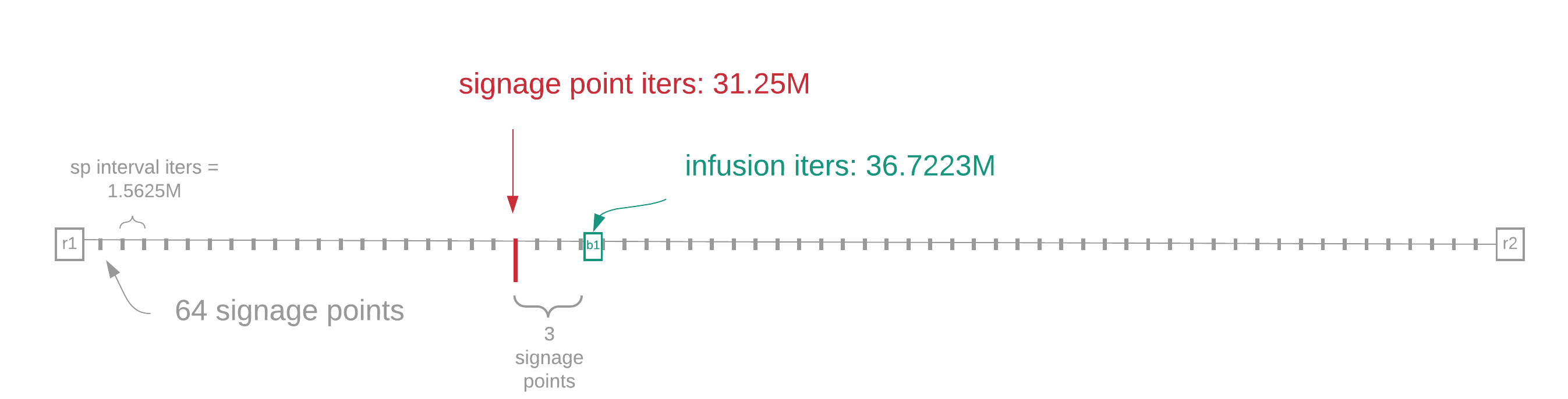
Figure 5: timelords create proofs for both the signage point and the infusion point. But they only infuse (change the VDF classgroup) for the latter. Squares symbolize infusions, where a new VDF is started.
Figure 5 shows the infusion point as a green square marked b1. The first and last blocks of the sub-slot are marked r1 and r2, respectively. For this example, the farmer will create the block at the time of the signage point marked with a red arrow, which we'll call b1'.
At b1, the farmer's block gets combined with the VDF output for that point. This creates a new input for the VDF from that point on, i.e. we infuse the farmer's block into the VDF. b1 is only fully valid after two events have occurred:
- infusion_iterations has been reached, and
- Two VDF proofs have been included: one from
r1to the signage point and one fromr1tob1. (Actually it's more since there are three VDF chains, explained in Section 3.8 'Section 3.8: Three VDF Chains')).
In Figure 5, the farmer creates the block at the time of the signage point, b1'. However, b1' is not finished yet, since it needs the infusion point VDF. Once the infusion_iterations VDF has been released, it is added to b1' to form the finished block at b1.
Recall that in this example,
- sub-slot_iterations = 100,000,000
- = (signage * point * sp * interval_iterations) + (3 * sp_interval_iterations) + required_iterations
For each of the 64 signage points, as they are released to the network every 9.375 seconds, or every 1.5625M iterations, the farmer computes the plot filter and sees how many plots pass. For each passing plot, the farmer calculates requirediterations. For each passing plot, the farmer calculates _required_iterations.
Let's say the farmer calculates requirediterations < 1.5625M once in the sub-slot. (We'll assume the exact required_iterations = 0.7828M in this instance.) Figure 5 shows this happening at the 20th signage point. (We'll assume the exact _required_iterations = 782,800 in this instance.) Figure 5 shows this happening at the 20th signage point.
infusion_iterations is then computed as:
infusion_iterations = signage_point_iterations + (3 \* sp_interval_iterations) + required_iterations
After realizing they have won (at the 20th infusion point), the farmer fetches the whole proof of space, makes a block (optionally including transactions), and broadcasts this to the network. The block has until infusion_iterations (typically a few seconds) to reach timelords, who will infuse the block, creating the infusion point VDFs. With these VDFs, the block can be finished and added to the blockchain by full nodes.
Rationale for choosing 64 signage points
Chia's original consensus, which was phased out before the launch of mainnet, used a single signage point per 10-minute subslot. This left the network vulnerable to short-range replotting attacks, where an attacker initiates a plot's creation after a signage point, and completes the plot before the next infusion point. The attacker could always choose a plot that passes the plot filter (because the signage point is hashed with the subslot challenge and the plot ID in calculating the filter) and then delete the plot after the infusion point. For a 512-filter, this would result in the attacker mimicking 512 plots (~51 TiB). In reality, under the original consensus, they would only need to own single computer capable of creating a plot in less than ten minutes.
Technically this isn't an attack because -- even if successful -- the "attacker" wouldn't gain an ability to cheat the network. However the "attacker" would be using the network in an unintended way, effectively turning Chia into a Proof of Work system. Therefore, Chia's new consensus was intentionally designed to discourage this behavior.
The new consensus was introduced during Chia's beta phase. One of the modifications was to increase the number of signage points to 64 per 10-minute subslot, or one every 9.375 (600/64) seconds, on average. The Challenge Chain was also introduced (see the Three VDF Chains page for more info). The maximum distance between a signage point and the next infusion point is now 4 signage points (see the infusion_iterations formula, above), or 37.5 seconds. This is the maximum amount of time for the attack to be possible, but for it to be consistently applied, the minimum time of 28.125 seconds must be applied. Assuming a few extra seconds for network latency and other factors, the attack is now only possible if one can create a new plot in less than 25 seconds.
Keep in mind that this "attack" is really mimicking the ownership of around 51 TiB of storage. Even when it does become possible to run the attack consistently, it will likely be much cheaper to use the network as intended, storing plots on non-volatile storage.
This begs the question: why not use even more signage points in the consensus? The simple answer is because as the signage points increase, it becomes more difficult for the timelords and nodes to keep up with the network. Sixty-four signage points per subslot was deemed enough to discourage the attack laid out above, while still allowing the timelords and nodes to perform as intended and to stay in sync.
Definitions
Quality string: A small part of the proof of space, 2 x values out of the total 64 x values, which can be retrieved efficiently from disk, and which values_to_fetch is determined by the signage point.
sp_quality_string: A hash of the quality string concatenated with the challenge chain's signage point. This hash is what ultimately decides the "luck" of a certain proof, using the size of requirediterations. This hash is what ultimately decides the "luck" of a certain proof, using the size of _required_iterations
sp_interval_iterations: Defined as floor(sub-slot_iterations / 64).
Signage points: 64 intermediary points in time within a sub-slot in both the challenge and reward chains, for which VDFs are periodically released. At each signage point, a VDF output is created and broadcast through the network. The first signage point in the sub-slot is the challenge itself. Each block has a signage point such that the proof of space in the block must be eligible for that signage point.
required_iterations: A number computed using the quality string, used to choose proofs of space which are eligible to make blocks. The vast majority of proofs of space will have requirediterations which are too high, and thus not eligible for inclusion into the chain. This number is used to compute the infusion point. The vast majority of proofs of space will have _required_iterations which are too high, and thus not eligible for inclusion into the chain. This number is used to compute the infusion point.
Infusion point: The point in time at infusioniterations from the challenge point, for a proof of space with a certain challenge and infusion_iterations. At this point, the farmer's block gets infused into the reward chain VDF. The infusion point of a block is always between 3 and 4 signage points after the signage point of that block. Computed as signage_point_iterations + 3 * sp_interval_iterations + required_iterations. At this point, the farmer's block gets infused into the reward chain VDF. The infusion point of a block is always between 3 and 4 signage points after the signage point of that block. Computed as _signage_point_iterations + 3 * sp_interval_iterations + required_iterations.
The delay between the signage point and infusion point has many benefits, including defense against orphaning and selfish farming, decreased forks, and no VDF pauses. This delay of around 28 seconds is given so that farmers have enough time to sign without delaying the slot VDF. Well-behaving farmers sign only one signage point with each proof of space, meaning that attackers cannot easily reorg the chain.