2 - Longest-Chain Protocols from Efficient Proof Systems

Before we can outline the specification of the $\textrm{{\sf Chia}}$ blockchain and its rationale in more detail, we first must understand the general challenges one faces when constructing a PoSpace based blockchain and some of the relevant literature on how to address these challenges.

Ultimately, we want to argue security assuming only that sufficient fraction of the resource (space, fast VDFs) is controlled by rational parties. Towards this, in this Section we first discuss how to achieve security assuming sufficiently many parties are honest, and then in §3 how rational behavior is incentivized by ensuring that deviating from the protocol will not give any (or very little) extra reward to parties. Towards this, in this Section we first discuss how to achieve security assuming sufficiently many parties are honest, and then in §3 how rational behavior is incentivized by ensuring that deviating from the protocol will not give any (or very little) extra reward to parties.

Figure 3: Illustration of the three main attack vectors that arise if we replace PoW with proofs of space (or any other efficient proof systems) in Bitcoin, and how they are addressed in Chia.

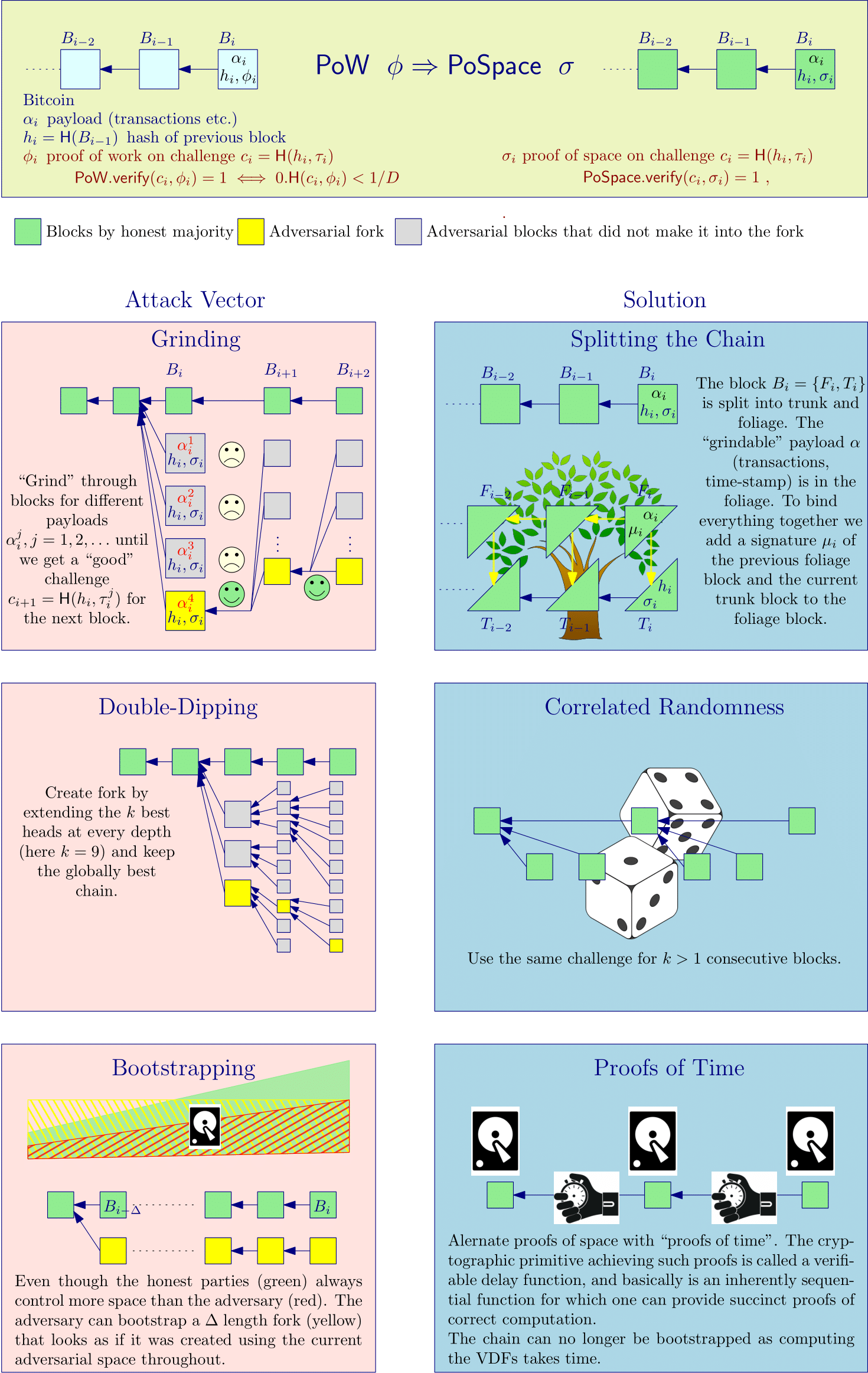
As mentioned in the introduction, just replacing proofs of work in Bitcoin with proofs of space does not work. For one thing, there are syntactic differences between proofs of work and proofs of space. But more importantly, security breaks down if one replaces PoW with PoSpace in any straight forward way. The reason for this is the fact that for PoSpace (after plotting) it's extremely cheap to compute a proof for a given challenge. The analogue issue with proof of stake is sometimes called "nothing at stake". We'll refer to proof systems where proofs can be efficiently computed (like proofs of space or stake) as efficient, and describe three attack vectors that arise because of this issue: grinding, double-dipping and bootstrapping. Those are illustrated in Figure 3 and described below. In §5 we'll describe how those attacks are addressed in $\textrm{{\sf Chia}}$ in more detail.

2.1 Grinding

In longest-chain blockchains the challenge used to determine the miner/farmer who can add a block is derived from the chain itself. In Bitcoin, where the challenge for a block is simply the hash of the previous block, a miner can influence the PoW challenge by trying out different transaction sets or time stamps. While such "grinding" through different challenges gives no advantage in PoW based cryptocurrencies, it's a problem once we use an efficient proof system.

To prevent such grinding we adopt an approach from Spacemint [PKF+18] and split the chain in two parts which we'll call trunk and foliage. The trunk contains only canonical proofs, and the challenges depend only on values contained in the trunk. This way the only choice a farmer has to influence the challenge is by withholding a winning block. The foliage contains all the remaining "grindeable" content, in particular transactions and time-stamps. The trunk contains only canonical proofs, and the challenges depend only on values contained in the trunk. This way the only choice a farmer has to influence the challenge is by withholding a winning block. The foliage contains all the remaining "grindeable" content, in particular transactions and time-stamps.

2.2 Double-Dipping

Even once grinding is no longer an option, an adversary can in private create an entire "block-tree" by forking at each level. While each path in such a tree will have an exponentially small (in the depth) probability of overtaking the honest chain if the adversary controls less than half the resources, there's also an exponential number of paths, so it's not clear how much of an advantage this strategy gives. For constructions where each challenge depends on the previous block (as in Bitcoin), it was shown [CP19] that this strategy "boosts" the resource by a factor $e\approx 2.718$, in particular, with this strategy an adversary (having an unlimited number of VDFs whose speed matches the fastest honest time lord) can create a chain that is longer than the honest one with only a $1/(1+e)\approx 0.269$ fraction of the total space, and thus significantly less than the $0.5$ fraction (of hashing power) required in Bitcoin.

To limit the impact of double-dipping an early version [CP19] of $\textrm{{\sf Chia}}$ consensus specified that also the honest parties do a very limited form of double-dipping and try to extend the best $3$ blocks they see at every depth, this rule was (by simulations) shown to increase the space required by an adversary from the $26.9\%$ mentioned above, to $38.5\%$.

The deployed $\textrm{{\sf Chia}}$ protocol uses correlated randomness to limit the impact of double dipping. The deployed $\textrm{{\sf Chia}}$ protocol uses correlated randomness to limit the impact of double dipping. This elegant idea was introduced in [BDK+19], and basically suggest to only use every $k$th block to compute the challenges.¹ The authors of [BDK+19] determine the exact fraction of the resource the adversary must control to break security as a function of $k$ (as mentioned, it's $2.718$ for $k=1$, and goes to $1$ as $k$ increases). $\textrm{{\sf Chia}}$ uses a variant where a challenge depends on one out of at least (not exactly) $k=16$ blocks. Their analysis also applies to this setting, and with $k=16$ states that by double dipping the adversary can boost their resource by a factor of $1.47$, which means they must control at least a $\frac{1}{1+1.47}=0.405$ fraction of the resource for an attack. $\textrm{{\sf Chia}}$ uses a variant where a challenge depends on one out of at least (not exactly) $k=16$ blocks. Their analysis also applies to this setting, and with $k=16$ states that by double dipping the adversary can boost their resource by a factor of $1.47$, which means they must control at least a $\frac{1}{1+1.47}=0.405$ fraction of the resource for an attack.

The resource considered in [BDK+19] is simply stake, while in $\textrm{{\sf Chia}}$ it's the product of space and VDF speed. Concerning VDFs, while for the honest parties the only thing that matters is the speed of the three VDFs controlled by the fastest honest time lord, for an adversary the speed as well as the number of VDFs available to them matter. In the security analysis we can simply assume the adversary controls an unbounded number of VDFs, as that's when the analysis from [BDK+19] applies. This is how eq.(2) $space_h\cdot vdf_h > space_a \cdot vdf_a \cdot 1.47$ in §1.1 was derived.

2.3 Bootstrapping

A major issue with longest-chain blockchains based on efficient proof systems is bootstrapping (aka. costless simulation) by which an adversary can use its resource to create a chain at basically no cost. Such bootstrapping can be used for short range attacks like selfish mining, but also long range attacks where an adversary forks the chain at a point in the past and then "bootstraps" it into the present. Such long range attacks make it hard to achieve security under dynamic availability, where we assume that the honest parties control a majority of the resource at any point in time, but the total resource can vary over time. The amount of hashing power contributed towards securing Bitcoin has varied by many orders of magnitude in the past, and the same already happened to $\textrm{{\sf Chia}}$ in the first weeks after launch.

Figure 4: Illustration of the no slowdown and delayed gratification properties. A longest-chain blockchain satisfying these properties is no more susceptible to selfish mining than Bitcoin.

Existing proposals to achieve security under such dynamic availability include check-pointing, which is problematic as parties that join for the first time or have not followed the chain for a longer period need additional trust assumptions to decide which chain to follow. Unlike for grinding and double-dipping, the attacks that become possible due to bootstrapping are quite different for proofs of space and proofs of stake. In the latter one must consider old keys that hold no stake in the current chain, but still can be used to bootstrap from a past block. To address this it was suggested to have honest parties use key-evolution schemes [BGK+18] so the current keys cannot be used to create blocks in the past. Key-evolution is problematic as it's clearly not rational for honest parties to do; they could sell their keys or lose their stake in case of a deep reorg.

The essence of the bootstrapping problem is the fact that one cannot ensure that time has passed in-between the creation of subsequent blocks. The essence of the bootstrapping problem is the fact that one cannot ensure that time has passed in-between the creation of subsequent blocks. $\textrm{{\sf Chia}}$ solves this problem by combining proofs of space with proofs of time, concretely, verifiable delay functions (VDFs), which enforce that some inherently sequential computation (which requires time linear in the length of the computation) was performed in-between the creation of blocks. $\textrm{{\sf Chia}}$ combines those three countermeasures (splitting the chain, correlated randomness and proofs of time) into a single design which is secure if the resources controlled by the honest parties satisfy the bound from Eq. $\textrm{{\sf Chia}}$ combines those three countermeasures (splitting the chain, correlated randomness and proofs of time) into a single design which is secure if the resources controlled by the honest parties satisfy the bound from Eq.

Footnotes

1. Using the same challenge for $k>1$ blocks has already been suggested in [PKF+18], but this is a different requirement (as the challenge can still depend on all blocks) and adds much less security than correlated randomness for small $k$. ↩