Skip to main content

4 - Hash and VDF chains

A key ingredient in longest-chain blockchains are hash-chains as discussed in §4.1 below. While Chia\textsf{Chia} also uses a hash-chain (for the foliage chain FC{\cal FC}), for Chia\textsf{Chia} we use a new chaining structure called a VDF chain defined in §4.2 below.

4.1 Hash chains​

For this writeup, a hash chain is a sequence b0,b1,b2…b_0,b_1,b_2\ldots of blocks, where each block bi={hi,xi}b_i=\{h_i,x_i\} contains some data value xix_i (possibly empty) and (with the exception of b0b_0) a hash value of the current data and the previous block.

hi:=H(bi−1,xi)h_i:={\sf H}(b_{i-1},x_i)

Security from hash chains.​

A hash chain is immutable in the following sense:

Proposition 2 (immutability of hash chains). If H{\sf H} is a collision-resistant hash function, then it is computationally infeasible to find two distinct hash chains H=b0,….bi{\cal H}=b_0,\ldots.b_i and H′=b0′,…,bj′{\cal H'}=b'_0,\ldots,b'_j where hi=hj′h_i=h'_j and no chain is a prefix of the other (which holds if they start with the same x0=x0′x_0=x'_0).

4.2 VDF chains​

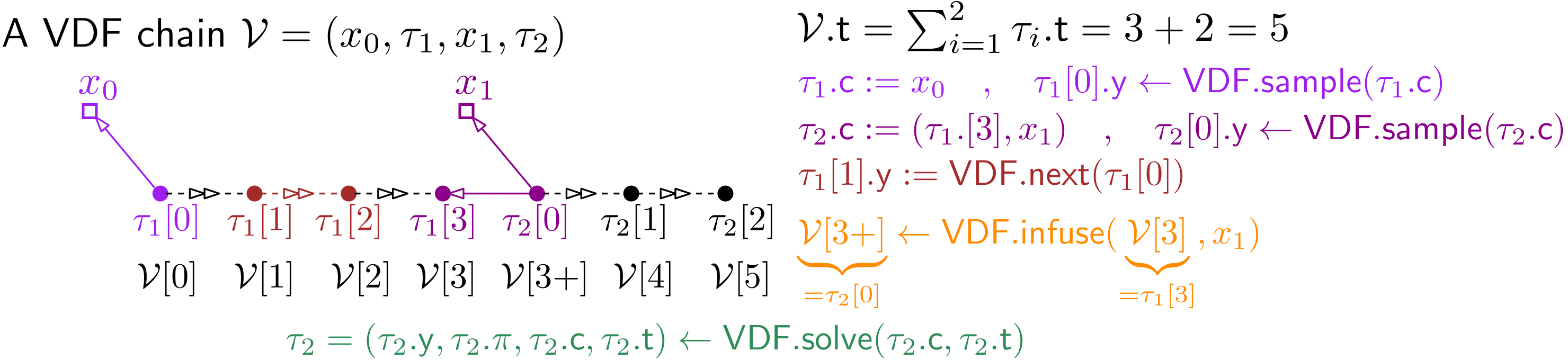
Illustration of a VDF chain
Figure 6: Illustration of a VDF chain.

A VDF chain is a sequence

V=z0,τ1,z1,τ2,z2,…,τℓ{\cal V}=z_0,\tau_1,z_1,\tau_2,z_2,\ldots,\tau_\ell
eq.(5)

alternating data values zi∈{0,1}∗z_i\in\{0,1\}^* and VDF values τi=(τi.y,τi.π,τi.c,τi.t)\tau_i=(\tau_i.{\sf y},\tau_i.\pi,\tau_i.{\sf c},\tau_i.{\sf t}) (as described in §A.3). The chain is valid if all VDF proofs are correct

VDF.verify(τi)=accept{\sf VDF.verify}(\tau_i)={\sf accept}

and the challenge for the iith VDF is derived from the previous VDF output (except for i=1i=1) and data value

τ1.c:=VDF.sample(z0) and ∀i>1:τi.c:=VDF.sample(τi−1.y,zi−1)\tau_1.c := \mathsf{VDF.sample}(z_0) \quad \text{ and } \quad \forall i > 1 : \tau_i.\mathsf{c} := \mathsf{VDF.sample}(\tau_{i-1}.\mathsf{y}, z_{i-1})

where we use the convention that τ0.y\tau_0.{\sf y} is the empty string.

4.2.1 Notation for VDF chains​

We naturally extend the notion for VDFs as described in §A.3 to VDF chains. The total number of VDF steps in a VDF chain as in eq.(5) is simply the sum of the steps in its VDFs

V.t=def∑i=1ℓτi.t{\cal V}.{\sf t}\stackrel{\scriptsize \sf def}{=}\sum_{i=1}^\ell \tau_i.{\sf t}

Security from VDF chains.​

VDF chains give two basic security guarantees, the first is immutability analogous to hash chains, but also sequentiality inherited from the underlying VDF, we discuss them shortly in more detail.

Proposition 3 (immutability and sequentiality of VDF chains). Like a hash chain, a VDF chain is immutable in the sense that it's computationally infeasible to come up with two different VDF chains

V=z0,τ1,z1,τ2,z2,…,τℓV′=z0′,τ1′,z1′,τ2′,z2′,…,τℓ′′{\cal V}=z_0,\tau_1,z_1,\tau_2,z_2,\ldots,\tau_\ell \qquad {\cal V}'=z'_0,\tau'_1,z'_1,\tau'_2,z'_2,\ldots,\tau'_{\ell'}

where the last VDF outputs collide, i.e., τℓ.y=τℓ′′.y\tau_\ell.{\sf y}=\tau'_{\ell'}.{\sf y}. Here different means that either they have different length ℓ≠ℓ′\ell\neq \ell' and neither is a prefix of the other. Or (if ℓ=ℓ′\ell=\ell') there exists an ii s.t. either zi≠zi′z_i\neq z'_i or τi.y≠τi′.y\tau_i.{\sf y}\neq \tau'_i.{\sf y} or τ.t≠τ′.t\tau.{\sf t}\neq \tau'.{\sf t}. Note that we ignore the proofs τ.π\tau.\pi when comparing chains (we just use them to determine whether the chain is valid) as they must not be unique.

Moreover a VDF chain is sequential, meaning that not only the individual VDFs must be computed sequentially (which follows from the security definition of VDFs), but also the VDFs in the chain were computed sequentially. I.e., computing a chain V{\cal V} as above requires ∑i=1ℓτi.t\sum_{i=1}^\ell \tau_i.{\sf t} sequential steps.