5 - The Blockchain
In this section we finally outline the design of the blockchain as illustrated in Figure 1 from its basic building blocks PoSpace, VDFs and Signatures. These primitives are specified in §A. We'll use greek letters to denote PoSpace, for VDFs and for Signatures.
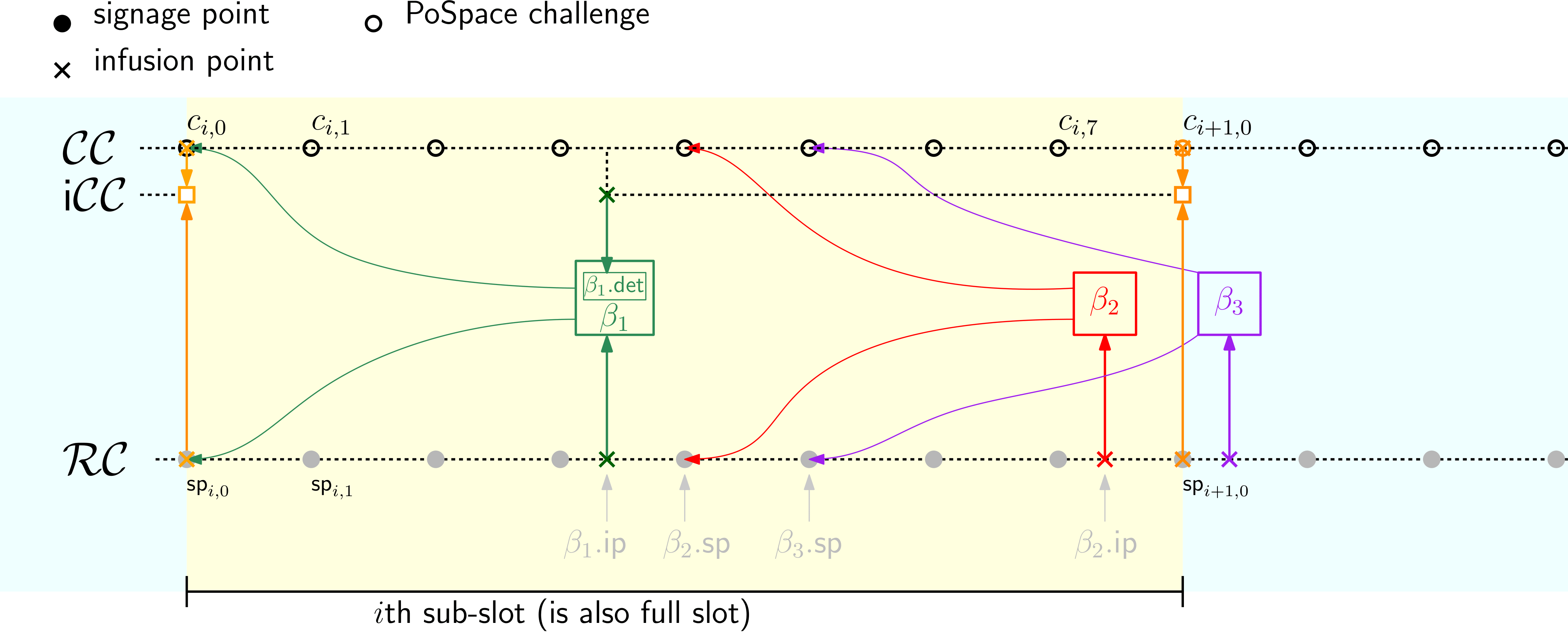
Figure 7: The reward, challenge and infused challenge chains. For illustration we only use 8 not 64 signage points per sub-slot.
5.1 Additional Variables and Notation for this Section
5.1.1 Variables
| Variable | Definition |
|---|---|
| Time parameter of -th slot (# of VDF steps per sub-slot). Recalibrated once per day for 10 minutes per sub-slot target. | |
| Difficulty parameter of -th slot. Recalibrated once per day for 32 blocks per slot target |
5.1.2 Step to Epoch
:Number of sub-slots in th slot. Typically but can be larger integer to enforce a block minimum.
5.1.3 Notation for Points of Interest
To describe the chains it will be convenient to introduce some extra notation. Recall that for a VDF or VDF chain we denote with or the point steps into the computation. is the total number of steps. Sometimes we overload notation and consider to denote the point at the end of the computation rather than the entire VDF or VDF chain, i.e., .
The VDF chains we'll consider ( and ) will be split into slots where the starting point of a new slot will always be an infusion point. For a point on such a chain we denote with
| Point | Definition |
|---|---|
| the total depth, i.e., the number of steps of this point since genesis | |
| the depth of this point in the current slot | |
| the depth of this point in its VDF | |
| the value of the VDF chain at this point | |
| a proof certifying the VDF computation up to this point | |
| If is an infusion point where some value gets infused, then we denote with the point before infusion, and with the point after infusion |
The following points on the VDF chains will be defined
| Point | Definition |
|---|---|
| The th challenge chain signage point in the th slot (eq.(6)) | |
| The th reward chain signage point in the th slot (eq.(9)) | |
| he used as challenge to compute the PoSpace in block | |
| The whose signature is in | |
| The infusion point of into (eq.(10) |
The signage point interval is the number of VDF steps between signage points, for the th slot it's
so e.g., the depth of the th signage point in the th slot is . A block in the th slot will be infused 3 to 4 signage point intervals past its signage point.
The first signage point in a slot is the last signage point after infusion
The th slot starts at total depth
5.2 The Challenge Chain
The challenge chain is a VDF chain whose data and VDF values we'll denote as
Here is the VDF computation for the th slot. Usually its number of VDF steps is the current time parameter (and should take 10 minutes to compute), but in exceptional cases it can be an integer multiple of that as we enforce a 16 block minimum per slot
The value infused at the beginning of slot depends on the first block in slot , we'll explain how exactly in §5.5.
As the VDF of the th slot is computed by a time lord, they release equidistant points of this computation called the challenge chain signage points, one every VDF steps or around seconds
The point at the end of the slot must also be broadcast as it's required to verify the VDF, but it's not used as a challenge as it's at the same depth as the first signage point of the next slot.
To get the security gains of correlated randomness, we let our PoSpace challenges depend on only one block (out of around 32) per slot, so there's a fresh challenge every 10 minutes. At the same time, we want a smooth continuous block arrival time (target is 18.75 seconds) and the challenge for each block should be revealed around 30 seconds before the block is infused (not much less to avoid orphan blocks, not much more to limit selfish mining and bribing opportunities). Deriving challenges deterministically from one initial challenge using a delay function as outline above achieves exactly that.
The reward chain is a VDF chain that the time lords evaluate in parallel to and also has signage points at the same depth as , i.e., . Before we can define we first need to explain the content of blocks.
5.3 Trunk Blocks {#S:TB}
Whenever a farmer receives new signage points they first check whether this points lie on a heaviest chain (cf. the discussion in §1.5) and their VDF proofs verify. If the this is the case, the farmer checks they can create a winning PoSpace proof. This process will, for a subset of the plots, produce a PoSpace and some additional value . Whether this PoSpace is a winning proof is now determined by the time parameter as
With our winning condition we have 32 blocks per slot in expectation depending on a challenge. We could have used a different design to enforce exactly 32 challenges, but then it would be impossible to achieve our Objective 1.(c), which asks that whether a plot wins must depend solely on the challenge.
If a farmer has a winning PoSpace they can produce a block which contains the foliage block and the trunk block . The actual blocks are more sophisticated than our description below, but in this writeup we focus on the entries which are absolutely necessary for functionality and security of the chain and ignore entries which are there for efficiency like weight proofs for light clients or pooling. They key entries in a valid trunk block
are
, a proof of space for some plot on challenge where the proof satisfies the winning condition from eq.(7).
, a signature using the secret key of the plot (so it verifies under the public-key in the PoSpace) of the signage point in the rewards chain discussed in the next section.
5.4 The Reward Chain
The reward chain is a VDF chain that time lords compute in parallel to . Like , can be spilt in a sequence of slots.
While in the th slot just contains a VDF and the value infused at the end, each slot of the chain
is a VDF chain with typically around infused values: around 32 blocks and at the end of the slot also the and points at the same depth. The signage points are
Where do Blocks get Infused.
Let be some valid block for challenge , its reward chain infusion point is then at depth
As is at most the infusion point is somewhere between 3 and 4 signage points past the signage point it refers to. That means we have somewhere from 28.125 to 37.5 seconds for a round trip from the time lord who gossips the signage point, to a farmer who computes and gossips a block, back to the time lord who then infuses the block.
5.5 The Infused Challenge Chain
Recall that the challenge chain is used to create PoSpace challenges, and we want these challenges to only depend on one block per slot. For this, at the end of the th slot we infuse the PoSpace from the first trunk block whose signage point is in the th slot into . We don't simply infuse , but to delay revealing the challenge for as long as possible and make sure it's buried deep in the chain when revealed, we run a VDF on top of to get the infused challenge value to be infused as defined in §5.2.
Concretely, the infused challenge of the th slot is the output of a VDF computation
on some challenge and time which are defined as follows.
Let be the first trunk block infused into the th slot past the 3rd signage point, using notion as in eq.(10)
now the challenge is derived from the PoSpace in this block and the value of at the depth of its infusion point
the number of steps is the the remaining number of VDF steps in the slot, so the value will be available at the end of the slot when it's required, but not earlier
We only use , not the entire trunk block , to compute the infused challenge . This is crucial to ensure that the challenges depend only on a single challenge per slot. Had we infused the entire (as we do into ), the challenges would depend on all blocks (as depends on which infuses all blocks) and we would not get security against double dipping.
Recall that by our Objective 1.(a) we want challenges to be only revealed when necessary and (b) to be immutable once revealed.
While (b) suggest to infuse the first possible block so it's buried once revealed, for (a) it would be better to use the latest possible block. We go with the first block to achieve (b), and by running a VDF on top of the block we also achieve objective (a).
The target number of blocks per slot is 32, and there's an upper bound of 64 and lower bound of 16. These bounds make some attacks more difficult. In normal deployment the number of blocks will be close to its expectation, so these bounds should basically never be reached. The lower bound is required to bound the efficacy of double-dipping as sketched in §2.2, while the upper bound is necessary to prevent replotting attacks as explained in §1.8.3.
To prevent grinding, the only decision that influences the trunk should be whether to add a block or not. We need one exception to this rule: the time-stamps (in blocks in the foliage) are used to recalibrate the time parameter which determines the numbers of VDFs steps per slot in the trunk. This gives a minor grinding opportunity, to further limit the usability of this for attacks, the window used to calibrate the time parameter is not simply the previous epoch, but shifted back so the relevant time-stamp is already buried deep in the chain.
To limit the impact of double-dipping we use correlated randomness [BDK+19]). For this the challenge chain should only depend on the first block in every slot. If this was the case, this would allow for long-range replotting attacks. For this reason, once every sub-epoch (approx 2h) the rewards chain is infused to the challenge chain.
5.6 The Foliage
Whenever a farmer finds a winning PoSpace they can create a block which contains the trunk block as discussed above, and a foliage block
which contains the payload of the block (transactions, a time-stamp) and a signature (using the key as for , cf.§5.3})
that links this foliage block to the chain. It signs the (hashes of the) current trunk block as well as the foliage block from the last transaction block as discussed below.
While every valid trunk block will typically be infused into (unless the time lord is malicious, the block arrives too late to be infused or the slot is already at its 64 block upper limit), only a subset of the foliage blocks are included in the foliage chain for reasons outlined below:
We want blocks to arrive at a rather high frequency ( seconds on average) to achieve fast confirmation. At the same time we want to give sufficient time ( to seconds between signage and infusion points of a block) for block creation to prevent oprhan blocks.
Every block of transactions added must refer to the previous block of transactions. This way we avoid having to deal with transactions that are invalid due to previous transactions that were added but were not known to the creator of the current transaction block.
To achieve the above objectives, we let farmers who found a winning PoSpace and can create a block always create a foliage block referring to the last transaction block before the signage point of their block. The time lord will add the foliage of a block – and thus make this block a transaction block – if no other transaction block was infused between the signage and infusion point of that block.
5.7 Fraction of Transaction Blocks
With the above rule, we expect one transaction block every slots, that's one every seconds and corresponds to of all blocks.
For the interested reader, let us shortly outline how the above is determined. The signage points of consecutive transactions blocks must be at least 4 points apart as a block with signage point is infused somewhere between and . The gap can be bigger than points if no block is found in response to and potentially more points after that. The expected number of blocks found for each slot is (32 block target for 64 points). The number of blocks found for each slot is Poisson distributed with expectation ( block target for points). With this distribution, the expected number of consecutive points with no blocks is .